安装及使用Q-Chem程序做Spin-Flip TDDFT计算寻找S0-S1极小能量交叉点
Installing and Searching for S0-S1 MECP with Spin-Flip TDDFT Method in Q-Chem
Jiawei Xu
Released: 2022-06-17 / Updated: 2022-06-17
0. 前言
寻找势能面之间的极小能量交叉点(Minimum Energy Crossing Point, MECP)是激发态研究中经常遇到的问题。使用CASSCF方法寻找MECP是比较理想的,但CASSCF计算量较大,且涉及活性空间选择等问题,使用起来不是很方便。目前流行的TD-DFT方法兼顾精度与速度,不少程序也支持在TD-DFT级别下寻找MECP点,例如GAMESS、ORCA、Q-Chem等,Gaussian也可以通过Harvey的MECP外置程序实现。GAMESS、ORCA等程序手册给出的是寻找S0-S1 MECP的例子,但实际上TD-DFT在描述参考态(S0)与激发态之间MECP时存在问题,这点已经在ORCA 5.0.2版本手册的8.3.12节中指出,不少文献也提及了这一观点,究其原因是TD-DFT方法下S0-S1 MECP的参考态波函数为单行列式波函数,但在MECP附近其多参考性不能忽略,故存在缺陷。在这一问题上,Spin-Flip TDDFT方法能够较好地弥补这一缺陷,尤其是对具有双自由基特征的体系表现极佳,结果与CASPT2接近,但计算量与TD-DFT相仿佛,可以处理较大的体系。本文通过几个计算实例简要介绍在Q-Chem程序中利用SF-TDDFT方法寻找MECP的做法。
1. SF-TDDFT方法的原理
SF-TDDFT方法通过翻转参考态波函数中的一个电子自旋给出单激发组态,激发态波函数由这些单激发组态线性组合而成,因此计算量与TD-DFT相仿佛。原理上也可以翻转多个电子自旋给出多激发组态,但这不是SF-TDDFT的范畴,此处不做讨论。常见的做法是通过翻转三重态参考态的一个\alpha电子自旋给出单重态,这时也称为Flip-Down TDDFT。对于这种情况,原先真正的基态S0可能会成为SF-TDDFT计算中的S1态,且由多个行列数线性组合描述,在一定程度上解决了普通TD-DFT计算MECP时的问题。
2. Q-Chem程序的安装
Q-Chem程序是收费程序,可以在官网上获取试用版本(https://q-chem.com/try/),试用期为两个月。进入这一链接后按要求填写相关信息,会收到Q-Chem公司的邮件,其中有与邮箱绑定的试用号。然后在官方链接中下载所需平台和版本的Q-Chem程序(https://q-chem.com/install/),按照教程安装。安装过程中会提示输入申请试用版本的邮箱和试用号,联网情况下程序会自动查询是否正确,正确则通过安装。对于网络异常导致的不能正常通过,一般可以使用科学上网方法,或者将license.data文件发邮件给Q-Chem客服,客服会另外发送与机器绑定的license,可用于进行离线安装。安装完成后在试用期内可以正常运行。
3. 实例
3.1 乙烯
乙烯双键的\pi轨道构成2e-2o活性空间,其S1态可以近似描述为\pi^1\pi^{*1}。乙烯双键旋转的过程中\pi键断裂,体系具有明显的双自由基特征,在两个亚甲基垂直的D2d群结构下(与丙二烯类似),S0-S1两态完全简并。在整个圆锥交叉(conical intersection, CI)空间里,S0-S1两态近简并。乙烯是最早使用SF-TDDFT考察的体系,在J. Phys. Chem. A, 2009, 113, 12749中研究了乙烯势能面上比较有实际意义的三个S0-S1 MECP点,即PY-、HM-和ET-MECP。在光引发情况下,乙烯可通过PY-MECP发生双键旋转,通过无辐射方式退激。
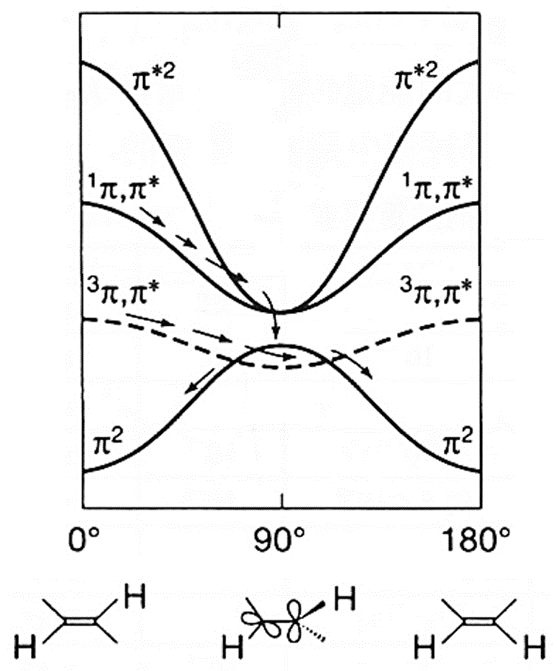
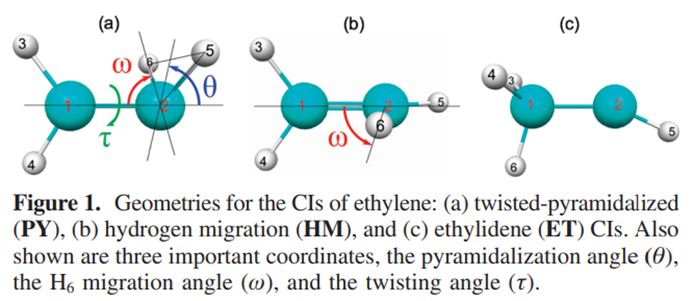
输入文件可以通过Q-Chem官方搭配的图形界面IQMol创建,可以在官网上免费下载(https://q-chem.com/try/iqmol/),也可通过其他常见的建模软件搭建并获得结构的三维坐标,然后手动写任务控制部分。由于一般最常用的量化计算软件是Gaussian,二者同宗同源,有许多相似之处,为了方便Gaussian用户快速上手Q-Chem,笔者整理了一些常用关键词的对照表可供查询(https://www.homechemer.com/computchem/2)。Q-Chem程序计算乙烯PY-MECP的输入文件如下:
$molecule
0 3
C -2.39240544 1.11077629 1.02316771
C -1.06648944 1.11077629 1.02316771
H -2.98599044 0.45738417 0.36977276
H -2.98602144 1.76413589 1.67656125
H -0.94047700 2.00850459 0.78262422
H -0.26589009 1.10234599 1.77493327
$end
$rem
GUI 2
JobType Opt
Method BHHLYP
Basis 6-31G(d,p)
MECP_Opt True
Spin_Flip True
CIS_N_Roots 5
MECP_State1 [0,1]
MECP_State2 [0,2]
MECP_Methods Penalty_Function
$end
需要注意的是,MECP优化显著依赖于初始结构。合理的初始结构有助于收敛到意义明确的MECP结构,如初始结构偏离较大,可能会收敛到CI空间内的其他MECP结构,其化学意义未必明确。用IQMol打开输出文件,可以看到最终优化得到的结构并不是D2d群,各C-H键均发生了一定的构象调整。也可以从输出文件中复制最后一帧结构,手动改成Gaussian的输入文件用GaussView查看。
用文本编辑器打开输出文件查看优化过程的输出,可以看到首先进行一次三重态基态的SCF计算,收敛结果的自旋平方算符期望值为2.004。
A unrestricted SCF calculation will be
performed using DIIS
SCF converges when DIIS error is below 1.0e-08
---------------------------------------
Cycle Energy DIIS error
---------------------------------------
1 -78.8706291302 4.96e-02
2 -78.3339923163 4.72e-03
... ...
12 -78.3717577980 1.35e-08
13 -78.3717577980 3.37e-09 Convergence criterion met
---------------------------------------
SCF time: CPU 14.92s wall 1.00s
<S^2> = 2.004181205
SCF energy in the final basis set = -78.3717577980
Total energy in the final basis set = -78.3717577980
然后进行激发组态的迭代,输出SF-TDDFT计算得到的激发态信息。第一激发态的自旋平方算符期望值为0.0236,可以指认为单重态。由于初始结构并不是乙烯的平面结构,故此时基态并不是\pi^2组态,而是^3\pi^1\pi^{*1}三重态,即平面结构下的T1态。此时的S1即为平面结构下的S0态,相应地有第三激发态为S2,对应于平面结构下的S1。第五激发态的自旋平方算符期望值为0.9960,有显著的自旋污染,虽然Q-Chem默认1.20为判断单重态和三重态的阈值,但自旋污染严重的情况说明已经不适合使用SF-TDDFT,此时的结果可能并不可靠,应该使用CASSCF等方法寻找交叉点。此处第五激发态的激发能远高于第一和第三激发态,故基本不会影响结果,可以忽略。如果在优化过程中出现被跟踪的两态自旋污染严重,应该及时停止计算,检查原因,或换用其他方法,一般0.50以下的自旋污染都可以忽略。Q-Chem也支持无自旋污染的spin-adapted spin-flip TDDFT (SA-SF-TDDFT),但经验表明SF-TDDFT无法研究的问题一般SA-SF-TDDFT也无法给出可靠结果,且后者没有解析导数,无法进行较大体系的结构优化计算。
---------------------------------------------------
SF-DFT Excitation Energies
(The first "excited" state might be the ground state)
---------------------------------------------------
Excited state 1: excitation energy (eV) = 0.6403
Total energy for state 1: -78.34822842 au
<S**2> : 0.0236
S( 1) --> S( 1) amplitude = 0.4762 alpha
S( 1) --> S( 2) amplitude = 0.1888 alpha
S( 2) --> S( 1) amplitude = 0.6421 alpha
S( 2) --> S( 2) amplitude = -0.5411 alpha
Excited state 2: excitation energy (eV) = 0.8027
Total energy for state 2: -78.34226003 au
<S**2> : 2.0024
S( 1) --> S( 1) amplitude = 0.7205 alpha
S( 2) --> S( 2) amplitude = 0.6639 alpha
Excited state 3: excitation energy (eV) = 2.0076
Total energy for state 3: -78.29797913 au
<S**2> : 0.0734
S( 1) --> S( 1) amplitude = -0.4295 alpha
S( 2) --> S( 1) amplitude = 0.7558 alpha
S( 2) --> S( 2) amplitude = 0.4664 alpha
Excited state 4: excitation energy (eV) = 4.3458
Total energy for state 4: -78.21205250 au
<S**2> : 0.0946
S( 1) --> S( 1) amplitude = -0.1710 alpha
S( 1) --> S( 2) amplitude = 0.9682 alpha
Excited state 5: excitation energy (eV) = 7.2166
Total energy for state 5: -78.10655438 au
<S**2> : 0.9960
D( 6) --> S( 1) amplitude = -0.2326
D( 7) --> S( 1) amplitude = -0.6558
S( 2) --> V( 1) amplitude = 0.6627 alpha
S( 2) --> V( 2) amplitude = 0.1619 alpha
然后进行弛豫密度的计算,接着Q-Chem输出有关基态波函数的一些基本信息,完成一次SF-TDDFT的单点计算。
接下来进行梯度计算。首先根据阈值选择被考察的两个单重态:A threshold of <S**2> = 1.20 is used to identify singlet states,可通过关键词CIS_S2_Thresh N (Threshold: N/100)来人为改变这一阈值。程序输出两态的基本信息及当前结构下两态的梯度矢量。
calculating CIS gradients for MECP_OPT
We are using <S**2> to determine which singlet excited state is the target state.
Determine which singlet state to optimize in UCIS or Spin-Flip UCIS
A threshold of <S**2> = 1.20 is used to identify singlet states
Excited state 1, <S^2> = 0.0236: is it a singlet? YES.
cis_state_deriv: 1
CIS relaxed dipole moment
1
1 0.0261541
2 -0.3558981
3 -0.0619512
Magnitude: 0.362 au 0.921 Debye
CIS 1 State Energy is -78.3482284193
Gradient of the state energy (including CIS Excitation Energy)
1 2 3 4 5 6
1 -0.1111696 0.0670777 0.0022334 0.0047943 0.0427766 -0.0057124
2 -0.0236528 -0.0465356 0.0075451 -0.0041807 0.1088581 -0.0420340
3 -0.0276008 -0.0882929 -0.0261074 0.0307093 0.1318372 -0.0205453
We are using <S**2> to determine which singlet excited state is the target state.
Determine which singlet state to optimize in UCIS or Spin-Flip UCIS
A threshold of <S**2> = 1.20 is used to identify singlet states
Excited state 1, <S^2> = 0.0236: is it a singlet? YES.
Excited state 2, <S^2> = 2.0024: is it a singlet? No.
Excited state 3, <S^2> = 0.0734: is it a singlet? YES.
cis_state_deriv: 3
CIS relaxed dipole moment
1
1 0.7909756
2 -0.6351955
3 0.0093171
Magnitude: 1.014 au 2.579 Debye
CIS 3 State Energy is -78.2979791254
Gradient of the state energy (including CIS Excitation Energy)
1 2 3 4 5 6
1 -0.0273931 0.0303176 -0.0014504 -0.0147586 0.0419712 -0.0286867
2 0.0259754 -0.1178143 0.0074983 -0.0027563 0.0588073 0.0282896
3 -0.0381684 -0.1256791 0.0297313 -0.0245972 0.1740429 -0.0153295
该任务输入中指定了使用惩罚函数(penalty function)方法优化MECP点,接下来计算惩罚函数等信息。Q-Chem没有现成的关键词可以修改惩罚函数方法的收敛标准(至少手册中没有给出),但从经验看来惩罚函数方法收敛精度并不高,但速度上具有一定优势,可以在结构偏离较大的情况下用来做初步优化。然后程序给出第一轮优化的结果。最后输出的收敛情况为3个NO,说明离优化收敛还差得很远。
** GEOMETRY OPTIMIZATION IN DELOCALIZED INTERNAL COORDINATES **
Searching for a Minimum
Optimization Cycle: 1
Coordinates (Angstroms)
ATOM X Y Z
1 C 0.6490763685 -0.0166246091 0.0267772021
2 C -0.6664681152 0.1458842232 -0.0046366466
3 H 1.3527261412 0.8242369730 -0.0366118550
4 H 1.1233438183 -1.0029680196 0.1183135498
5 H -0.8385958381 -0.3674310196 -0.7704929744
6 H -1.5331236410 -0.2293956186 0.5559479467
Point Group: c1 Number of degrees of freedom: 12
Energy is -78.323103772
Attempting to generate delocalized internal coordinates
Initial Hessian constructed with Jon Baker's OPTIMIZE code
12 Hessian modes will be used to form the next step
Hessian Eigenvalues:
0.032207 0.032207 0.058678 0.160000 0.160000 0.160000
0.160000 0.338745 0.338749 0.338749 0.604807 0.605119
Minimum search - taking simple RFO step
Searching for Lamda that Minimizes Along All modes
Value Taken Lamda = -0.46930849
Calculated Step too Large. Step scaled by 0.336864
Step Taken. Stepsize is 0.300000
Maximum Tolerance Cnvgd?
Gradient 0.280807 0.000300 NO
Displacement 0.156529 0.001200 NO
Energy change ********* 0.000001 NO
优化收敛后输出结果如下,可以直接用IQMol查看,或者复制这一结构并将其改写成其他可视化程序可识别的格式,用其他程序查看。
******************************
** OPTIMIZATION CONVERGED **
******************************
Coordinates (Angstroms)
ATOM X Y Z
1 C 0.6076202045 0.0099562520 0.0711311781
2 C -0.7414129227 0.3051250047 -0.0214996635
3 H 1.3765169742 0.7735724304 -0.0381247666
4 H 1.0503425185 -0.9911489616 0.1520435281
5 H -0.8384996307 -0.4170582242 -0.8981561847
6 H -1.3676084101 -0.3267445721 0.6239031312
注意查看最后一次输出的SF-TDDFT结果,检查是否合理。对于本例,最后一步输出的结果显示第二和第三激发态为被考察的两个单重态,自旋污染不严重,说明SF-TDDFT能够基本正确地给出结果。两态激发能分别为0.9202 eV和0.9346 eV,比较接近,但仍有一定能隙,这是因为Q-Chem中惩罚函数方法默认的收敛精度不够高所致,可以在惩罚函数方法的优化基础上继续用分支平面递推方法(branching plane updating method, BPUPD)进一步优化,关键词为MECP_Methods Branching_Plane。
---------------------------------------------------
SF-DFT Excitation Energies
(The first "excited" state might be the ground state)
---------------------------------------------------
Excited state 1: excitation energy (eV) = 0.8273
Total energy for state 1: -78.35539548 au
<S**2> : 1.7606
S( 1) --> S( 1) amplitude = 0.3977 alpha
S( 2) --> S( 2) amplitude = 0.8950 alpha
Excited state 2: excitation energy (eV) = 0.9202
Total energy for state 2: -78.35197980 au
<S**2> : 0.2504
S( 1) --> S( 1) amplitude = 0.8678 alpha
S( 2) --> S( 2) amplitude = -0.4047 alpha
Excited state 3: excitation energy (eV) = 0.9346
Total energy for state 3: -78.35145141 au
<S**2> : 0.0974
S( 2) --> S( 1) amplitude = 0.9829 alpha
Excited state 4: excitation energy (eV) = 5.6717
Total energy for state 4: -78.17736611 au
<S**2> : 0.1993
S( 1) --> S( 2) amplitude = 0.9757 alpha
Excited state 5: excitation energy (eV) = 6.0180
Total energy for state 5: -78.16464165 au
<S**2> : 0.9844
D( 5) --> S( 1) amplitude = -0.1790
D( 7) --> S( 1) amplitude = 0.9317
S( 2) --> V( 1) amplitude = 0.1706 alpha
类似地也可以使用SF-TDDFT优化乙烯其他的两个MECP结构。
3.2 偶氮苯
偶氮苯衍生物也是典型的光异构化体系,光照可以引发N=N旋转,经过圆锥交叉空间发生无辐射退激。对于乙烯的例子,反应物和光产物相同,基态势能面是对称的,而对于本例基态势能面是不对称的,偶氮苯的反式构型更稳定。
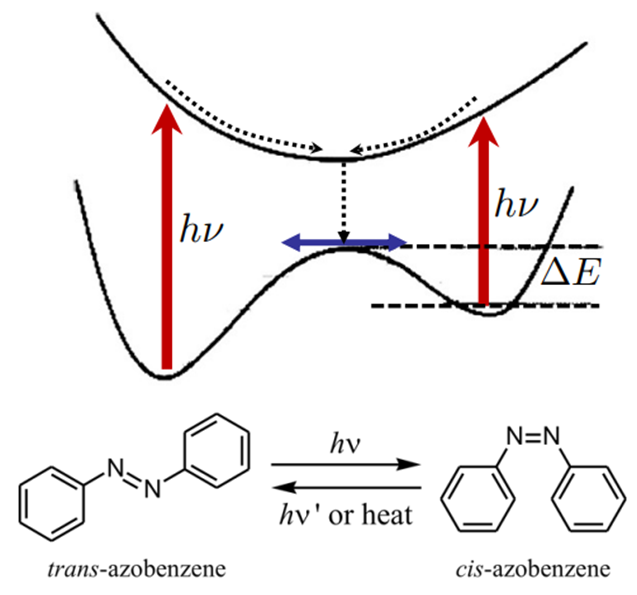
这里使用BPUPD方法寻找MECP。需要注意的是,BPUPD方法寻找MECP必须在笛卡尔坐标系下进行,输入文件中必须声明Geom_Opt_Coords 0。
$molecule
0 3
C -4.0110072727 0.8867526059 0.3687781802
C -3.8222885520 0.1505268061 -0.7936223690
C -2.6476065948 -0.5326805745 -1.0177433591
C -1.6206000793 -0.4914864252 -0.0630824037
C -1.8025446291 0.2696971939 1.1048807371
C -2.9921416581 0.9396982830 1.3075866152
H -4.9389392307 1.4045952162 0.5425163975
H -4.6023457015 0.1088998387 -1.5365103065
H -2.4981195408 -1.1066786311 -1.9158632277
H -1.0117017289 0.3146118162 1.8336312773
H -3.1220771286 1.5114085108 2.2141869803
N -0.4855558694 -1.1909791741 -0.2754674856
N 0.5912930884 -1.4021822808 0.3187355517
C 1.6830154825 -0.5736601800 0.0500793982
C 2.8250095993 -0.7988856552 0.8166873615
C 1.6672547417 0.4438601437 -0.9078788565
C 3.9293339675 0.0128224074 0.6567958452
H 2.8080105108 -1.5984694578 1.5366698658
C 2.7831903508 1.2382719085 -1.0704928250
H 0.7876846961 0.5858991456 -1.5116494451
C 3.9108653261 1.0314856400 -0.2852427246
H 4.8062044477 -0.1459567658 1.2605555974
H 2.7786628938 2.0217713704 -1.8113373491
H 4.7759979864 1.6594860134 -0.4170191124
$end
$rem
GUI 2
JobType Opt
Geom_Opt_DMax 50
Geom_Opt_Coords 0
Method BHHLYP
Basis 6-31G(d,p)
Spin_Flip True
CIS_N_Roots 5
MECP_Opt True
MECP_State1 [0,1]
MECP_State2 [0,2]
MECP_Methods Branching_Plane
$end


