使用PySCF程序做CASSCF和MC-PDFT计算
CASSCF and MC-PDFT Calculations Using PySCF Program
Jiawei Xu
Released: 2024-08-09 / Updated: 2024-08-30
MC-PDFT (multi-configuration pair density functional theory)是最近几年逐渐兴起的CASPT2和NEVPT2的平替方法,耗时相比后两者明显降低,但精度却损失不明显,目前主要被OpenMolcas、PySCF-forge和GAMESS等程序所支持。本文讲解PySCF程序结合PySCF-forge扩展包做MC-PDFT计算的基本方法,但由于MC-PDFT计算的难点主要是在CASSCF计算部分,故本文实际上重点讲解PySCF做CASSCF计算的方法,部分流程会使用到MOKIT程序作为协助。
1. 离线安装PySCF和PySCF-forge扩展包
对于有root权限、在线安装的情况:
pip install pyscf
pip install pyscf-forge对于最一般的、无root权限、离线安装的情况,推荐使用Anaconda Python。首先在一台能联网的机子上安装与集群相近版本的Anaconda Python,并下载PySCF及其必要依赖的安装包:
pip download pyscf
pip download pyscf-forge上述命令将会下载得到一系列的.whl安装包,将之上传至集群。我们选择使用Anaconda Python,由于PySCF是比较常用的库,可以直接安装在base环境。首先激活base环境,然后使用pip安装:
source ~/programs/Anaconda3/bin/activate base
which pip # 确认pip路径,此时应对应于~/programs/Anaconda3/bin/pip,默认安装至~/programs/Anaconda3/lib/python3.X/site-packages
pip install pyscf-2.xxx.whl2. 简单CASSCF计算
2.1 苯
苯分子基态的活性空间一般选为(6o,6e),即包含全部6个π轨道和6个π电子。该计算可直接使用MOKIT中的automr程序全自动完成,输入文件如下(原子坐标略):
%nprocshared=28
%mem=84GB
#p CASSCF/def2SVP
mokit{}
0 1
[Cartesian Coordinates]注意:def2-SVP基组对于CASSCF计算而言太粗糙,此处仅作为演示时使用,该任务不到一分钟就能迅速算完。
苯分子比较简单,所以使用默认的设置即可。MOKIT会首先对所提供结构进行RHF和UHF计算,并根据能量判断体系为闭壳层或开壳层。对于闭壳层的情况,会首先对虚轨道进行投影,然后做定域化,并匹配成键和反键轨道。对于开壳层的情况则是基于UHF波函数得到UNO (unrestricted natural orbital),然后匹配成键和反键轨道。基于此,调用GAMESS(或Gaussian)做广义价键计算(generalized valence bond, GVB),并将收敛的GVB波函数作适当处理选出活性空间,传递给PySCF进行CASSCF计算。本例MOKIT自动选出的活性空间即为(6o,6e),计算完成后得到一系列的输出文件。

观察ph_uhf_gvb15_CASSCF_NO.fch中的轨道,可见活性空间内的NO均为非整数占据,总占据数为6,其等值面图像也符合苯环π轨道的图像:
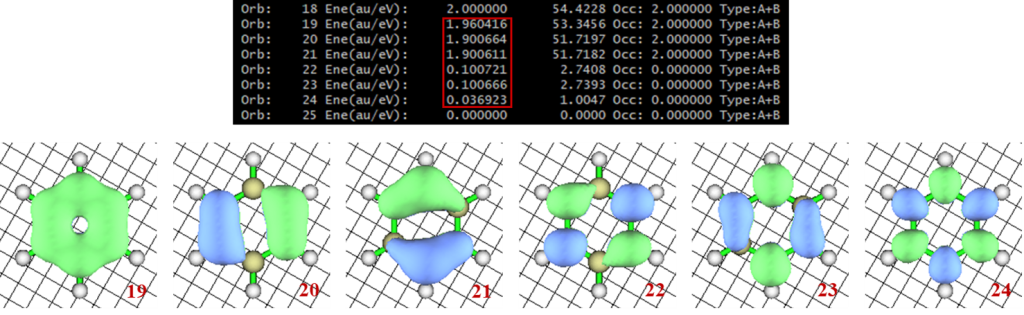
我们简单讲解一些有关轨道自动选择的计算细节。相比于Full CI,CASSCF实际上是选择一部分最具化学意义的轨道和电子作为活性空间,在活性空间范围内做Full CI。与之类似,GVB实际上也是针对一部分成反键轨道对进行有限范围内的VB计算,因此GVB轨道对也可以看做是某种意义上的活性空间。
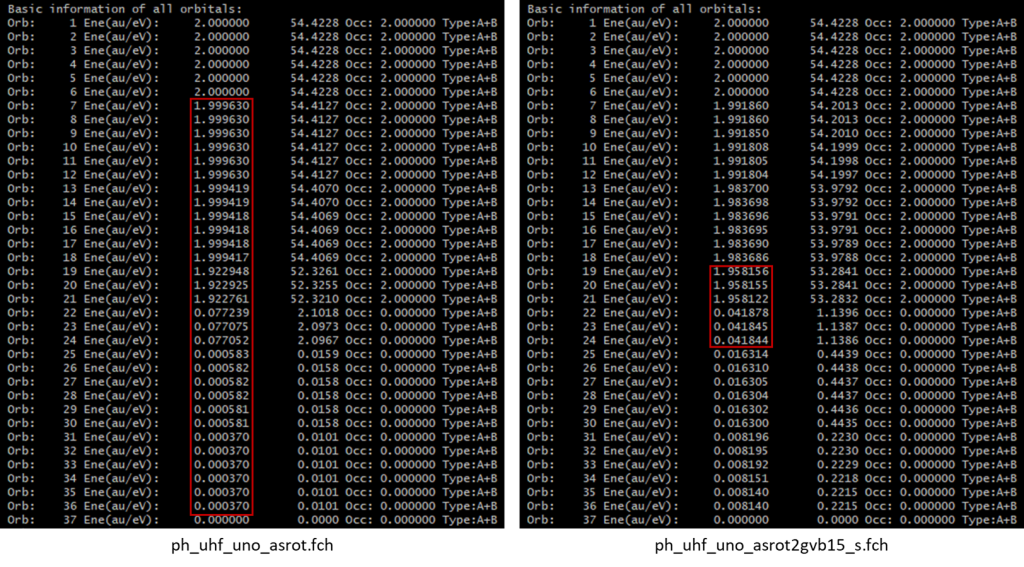
在由UNO向GVB传递初猜时,MOKIT默认选择占据数超过10-5的空轨道,也即ph_uhf_uno_asrot.fch中的22~36号轨道,将其以及与其一一对应的7~21号占据轨道全部纳入GVB活性空间,共15对GVB轨道对,故后续文件命名使用”gvb15″。这个标准很严格,绝大多数情况下实际上已经包含了所有的价层轨道。这个阈值可以通过关键词修改,如uno_thres=0.001则会将此标准放宽至0.001。如果采用0.001的阈值,GVB计算将仅限于π轨道,即ph_uhf_uno_asrot.fch中的19~24号轨道,对于本例来说实际上影响不大,因为苯环价层轨道中的其他C-C C-H σ轨道本身多参考性就几乎可以忽略。此外,也可以通过excludeXH关键词直接去除GVB计算中的C-H键轨道。
类似地,在由GVB向CASSCF传递初猜时,也是通过占据数决定活性空间所包含的轨道范围。MOKIT默认将占据数在0.02~1.98范围内的轨道全部纳入考虑,但这一范围没有现成的关键词可以修改(至少对于撰文时是如此)。这就对应于ph_uhf_uno_asrot2gvb15_s.fch中的19~24号轨道,恰好是所有的π轨道。也可以在GVB完成后终止计算,并通过关键词on_thresh=0.01,readno=”ph_uhf_uno_asrot2gvb15_s.fch”,ist=5以NO的形式读取GVB波函数,并取0.01作为占据数偏离0和2的阈值。
2.2 苯酚
仅考虑苯的部分,活性空间仍为(6o,6e),但考虑到氧原子的LP电子会与π键产生一定程度的共轭,选择(7o,8e)的活性空间似乎更妥。但由于MOKIT程序是成对地构建初猜波函数,因此实际上只能计算活性轨道数和活性电子数相等,即(no,ne)的情况,因此不可能选出(7o,8e)的活性空间。我们首先仿照2.1中做法使用MOKIT程序自动做CASSCF计算,可以看到所选出的活性空间仍为(6o,6e),包含23~28号轨道,而氧原子的LP轨道为20号轨道,不在活性空间的范围内。这是由于在GVB计算结果中,氧原子LP轨道的占据数不在默认的0.02~1.98范围内,因此被排除出了活性空间。

我们当然可以读取GVB波函数,并通过on_thresh来调整活性空间的范围,但这会同时考虑不必要的其他一些轨道,增大计算量。这时候就需要人为地调整轨道顺序。首先我们要理解PySCF的输入文件中如何定义活性空间:mcscf.CASSCF(m,(na,nb))表示活性空间包含m个空间轨道,na个α电子和nb个β电子,此时活性空间实际上是包含了前线轨道附近的这部分轨道和电子。对于单重态的苯酚,mcscf.CASSCF(6,(3,3))就对应于HOMO-2、HOMO-1、HOMO、LUMO、LUMO+1和LUMO+2及3个α电子和3个β电子。因此,额外包含氧原子的LP轨道后,活性空间的定义变为mcscf.CASSCF(7,(4,4)),同时我们还需要将20号轨道与22号轨道调换顺序,行列式波函数的性质决定了调换轨道顺序仅改变符号,而不改变波函数其他性质。使用Multiwfn的主功能6调换顺序,并将其重新保存为exchanged.fch文件:
Multiwfn phenol_uhf_gvb16_CASSCF_NO.fch
6
29
20,22
-1
100
2
7
exchanged.fch
0
q测试表明,Multiwfn生成的这个fch文件并不能被PySCF正确读取,确切地说是不能被PySCF输入文件中所调用的MOKIT中提供的fch2py函数正确读取。无妨,我们可以用Gaussian整理其文件格式,先转换为.chk格式:
unfchk exchanged.fch exchanged.chk编写如下Gaussian输入文件,并运行之,该任务会迅速完成:
%chk=exchanged.chk
#p ROHF/def2SVP guess=(read,only) geom=allchk nosymm int=nobasistransform注意上述任务需要保持基组与此前的计算均一致。得到新的.chk文件后,再转换为.fch格式即可,此时我们就得到了一个可以正确被py2fch读取的.fch文件作为初猜了。由于前面已经进行过活性空间(6o,6e)的CASSCF计算,因此实际上只需要基于此前的PySCF输入文件修改活性空间定义和初猜波函数文件名即可。执行该活性空间(7o,8e)的CASSCF计算,观察所得波函数就会发现,氧原子的LP轨道相较于纳入活性空间前发生了明显的变化,而其他π轨道也由于共轭都掺入了一定LP轨道的成分。

比较两次计算得到的CASSCF能量:CASSCF(6,6) -305.406703386517 a.u.;CASSCF(7,8) -305.407351500871 a.u. 可见扩大活性空间后能量有所降低,但由于LP轨道与π轨道的共轭程度较小,能量差异并不明显。一般来说,都要求活性空间的大小相同时才可以比较能量。也可以查看CASSCF(7,8)计算的第一轮迭代的能量,即初猜波函数CASCI的能量为E0 = -305.407324890267 a.u.,这就指明了同一波函数在不同活性空间下所得的能量是不可比较的。同时,E0与CASSCF(7,8)最终收敛的能量之间的差值也可以看做是由LP轨道与π轨道共轭所带来的能量降低。
使用MOKIT调换轨道顺序
MOKIT有一内置的permute_orb函数也可用于调换轨道。编写一个python文件:
from mokit.lib.gaussian import permute_orb
permute_orb('ethanol_rhf_proj_loc_pair2gvb8_s.fch',6,13)运行即可调换指定文件中两个轨道的顺序,轨道编号从1开始。也可以将此直接写进PySCF做CASSCF计算的输入文件。
2.3 二茂铁
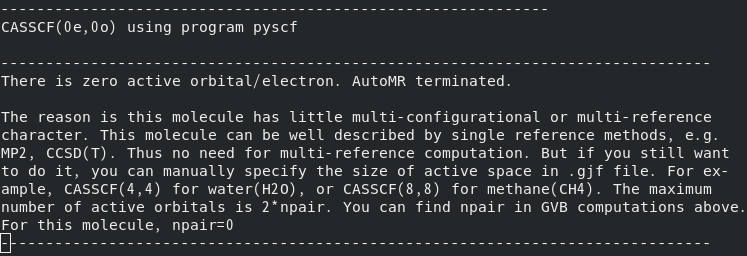
在PBE0-D3(BJ)/def2-SVP下优化得到二茂铁的极小点结构,并使用MOKIT做默认的CASSCF计算,将得到以下结果。这是由于在收敛所得的GVB波函数中并没有占据数介于0.02~1.98之间的轨道,因此没有轨道被选入活性空间。一般来说,这表明当前计算的体系多参考性较弱,使用CASSCF计算的意义不大。
即便如此,我们也依然可以使用CASSCF方法计算二茂铁的电子结构,最理想的活性空间应当包含Fe的全部5个3d轨道,以及两个环戊二烯负离子的10个π轨道,总共有18个电子占据,则活性空间的大小为(15o,18e)。首先通过观察GVB轨道的图像确认这15个轨道的序号,如下图所示。如何迅速选中这些轨道,这里就本例而言谈一种策略:
① 22~24号轨道是Fe的3d6轨道,从配体场理论(ligand field theory, LFT)的角度而言,这三个d轨道不与配体的轨道发生混合,因此表现为LP轨道,因而也易于从图像直接辨认。
② 36/46/48和35/37/47分别是上下两个环戊二烯负离子的π轨道。
③ 根据价键理论的思想,每个成键轨道都应对应于一个反键轨道,相应地就有49/51/61和50/60/62为其反键轨道,因为在MOKIT处理过的GVB波函数中,轨道按占据数排序,因而成反键轨道的序号恰好是关于HOMO-LUMO (48-49)对称分布的。但这就会产生12个π/π*轨道,这是不符合常理的。实际上这里的6个“π轨道”已经不是单纯的π轨道,而是非占据d轨道和π轨道相互作用产生的成键轨道,反键轨道似此,只不过部分轨道仍然很大程度上保留了π/π*轨道的图像,即只有36/61和35-62两组有明显的d-π图像性质。具体可参考配体场理论以及群论的内容。
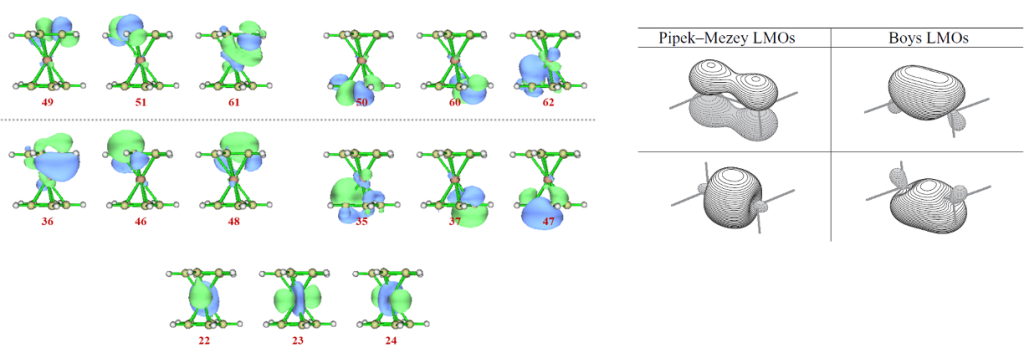
值得一提的是,GVB波函数中环戊二烯负离子的π轨道并不是传统观点中“肩并肩”的图像(即类似于图中的Pipek-Mezey LMOs),此处更接近于Boys LMOs的双键图像。Pipek-Mezey LMOs呈现的C-C双键的结果更符合化学直觉,Boys LMOs则将此处理成了两个等价的香蕉键。这两种双键的描述形式没法说谁对谁错,从物理角度上是等价的描述,只是恰巧对于本例来说,GVB波函数的结果与Boys的结果更接近。明白这一点,对于确定需要纳入活性空间的轨道序号很重要。事实上在双占据轨道中,每个环戊二烯负离子能够找到8个图像似此的轨道,显然,其中占据数更接近于2的5个轨道对应于C-C σ轨道,占据数偏离2较多的3个轨道为π轨道。
我们需要将这15个轨道通过调换顺序使之位于前线轨道,此时需要多次调换才能完成,此处提供一个一键调换轨道顺序的小程序exmo.py。运行之,得到重新排序后的波函数文件:
python exmo.py ferrocene_uhf_uno_asrot2gvb29_s.fch "22-24 35-37 46-48 49-51 60-62"然后使用所得的exchanged.fch作为初猜,仿照2.1和2.2中做法使用Gaussian处理文件格式问题,然后进行CASSCF计算。先产生含有分子结构、基组等基本信息的PySCF输入文件:
bas_fch2py exchanged.fch这将会得到一个新的名为exchanged.py的PySCF输入文件。仿照2.1和2.2中做CASSCF计算的输入文件,补充开头import以及CASSCF计算的部分代码即可提交任务。此外,本例所选的(15o,18e)活性空间虽然足够完善,但计算量较大,这样尺寸的活性空间一般可以做DMRG-SCF以节省计算量。
3. 为反应过程拟定统一的活性空间:基于GVB波函数
由于为了比较不同中间体/过渡态的能量,使用多参考方法计算更精确的电子能量时,必须保证活性空间的尺寸一致,且活性空间内所包含的轨道相近。我们以Phys. Chem. Chem. Phys., 2020, 22, 17677-17686中所研究的Fe催化交叉偶联反应为例,讲解如何为不同结构选择尽量统一的活性空间。首先使用SI中所提供的结构,在PBE0-D3(BJ)/def2-SVP级别下重新优化,在优化完毕的结构基础上,使用MOKIT做自动GVB/def2-TZVP计算。该反应如下:
3.1 RC (S = 3/2)
根据GVB结果,占据数介于0.02-1.98范围的轨道包含以下13个。可以发现,102-105和111-114是4个苯基阴离子的4对π/π*轨道,106和110是Fe-C配位键的σ/σ*轨道,且具有形似d轨道的成分,107-109是3个单占据的d轨道。

我们首先将我们的结果与原文献中的(21o,21e)活性空间对比。原文首先基于UKS波函数得到了UNO波函数,然后根据NOON (natural orbital occupation number)介于0.03-1.97的阈值选择活性空间,共包含了4个苯基阴离子的共8对π/π*轨道和5个3d轨道,并将此活性空间尺寸应用于其他中间体和过渡态,以收敛的CASSCF波函数做NEVPT2计算以获得准确的电子能量。我们不讨论该工作流程是否合适,仅思考这部分轨道是否适用于整个反应。
这里计算的实际上是交叉偶联反应中的还原消除步骤,因此偶联两个芳环的孤对电子,其中一对形成Ar-Ar键,另一对转移给Fe(III)形成Fe(I)。故活性空间必须包含这一部分轨道才能够准确描述反应过程,并给出可比较的电子能量。但在原文的(21o,21e)活性空间中,这一部分轨道却并未完全考虑到。同时我们会注意到,在原文使用UKS得到的UNO波函数中,Fe-C配位键比较彻底地被划分成d轨道和LP轨道,因此LP轨道(的成分)并未出现在活性空间中。
GVB波函数的结果如何呢?如图所示,106和110轨道是我们需要考虑的Fe-C键轨道,但不是实际发生反应的一组,我们希望考察的交叉偶联反应涉及带有氨基取代的苯基阴离子及其邻位的苯基阴离子。GVB轨道占据数0.02-1.98的范围内并未包括我们希望得到的两对轨道,可能原因是处于氨基苯基阴离子对位的苯基阴离子受其影响,轨道占据数刚好位于范围之内。但这并不重要,我们可以很容易辨认出46、47、58、106、110、158、169和170是4对Fe-C成反键轨道。
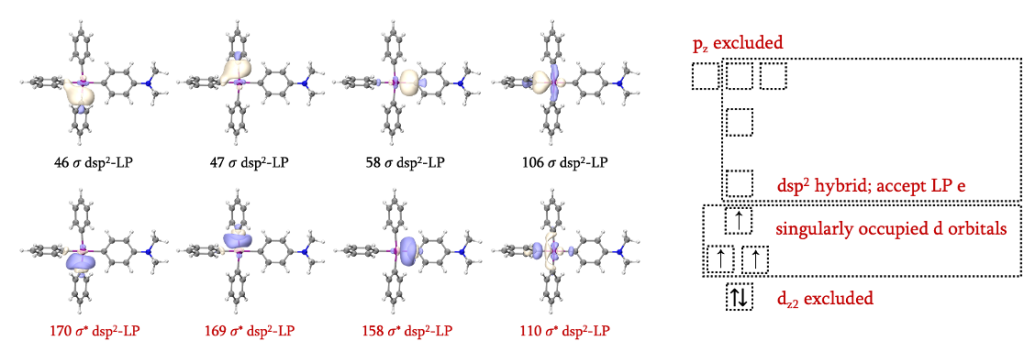
现在我们自然而然就会产生一个疑问。观察图中的这些Fe-C键轨道,他们都表现出d轨道的成分。理论上来说,若d轨道与LP轨道形成配位键,4对Fe-C键轨道就要涉及到4个d轨道,加上单占的3个d轨道 (107-109),总数达到了7个,这是违反常理的。如何理解这一情况呢?配体场理论指出,对于平面四方形场,用于成键的d轨道只有一个,此处即为dsp2杂化,同时还有1个4p轨道未参与杂化。因此,当我们考虑任何一个Fe-C键时,我们就必要要考虑所有4个Fe-C键,这也就同时考虑了Fe原子9个价层轨道中的7个。而dz2和pz在该反应中并未涉及,故排除在活性空间之外。这也告诉我们,在选择d区金属原子的活性空间时,并不总是需要将所有的d轨道纳入活性空间考察(虽然很多文献都这么做),考虑计算成本时,可以根据实际情况删减不重要的轨道。
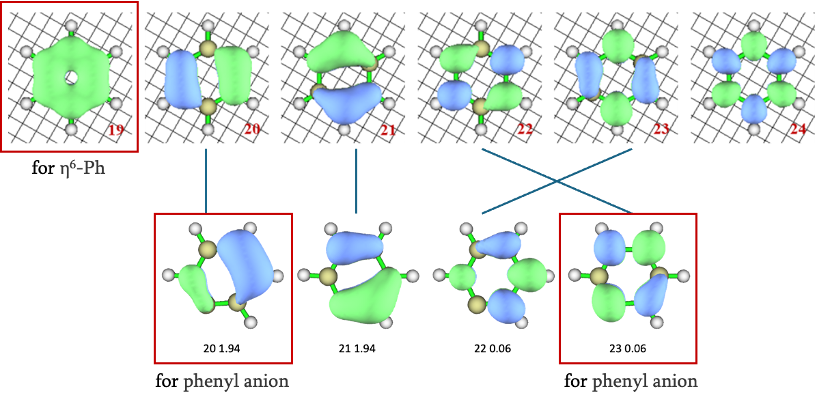
接下来我们讨论配体的π/π*轨道。在此之前,我们不妨对比一下基于GVB轨道占据数给出的苯环与苯基阴离子的活性空间。相较于苯环的6个π/π*轨道,苯基阴离子GVB轨道占据数介于0.02-1.98之间的仅有四个轨道,其与苯环的π/π*轨道的对应关系如图所示。苯基阴离子具有较强多参考性的20/23轨道,正对应于RC (S = 3/2) 所得GVB轨道的102-105和111-114。相应地,我们也可以在GVB轨道中找到21/22所对应的另外4对π/π*轨道。由于苯基阴离子仅以LP轨道配位,π/π*轨道仅于金属中心原子有较弱的d-π共轭,因此仍然保留了孤立苯基阴离子中的轨道图像,容易辨认出84、98、100、101、115、116、118和132轨道是我们想找出的第二组共8个π/π*轨道。
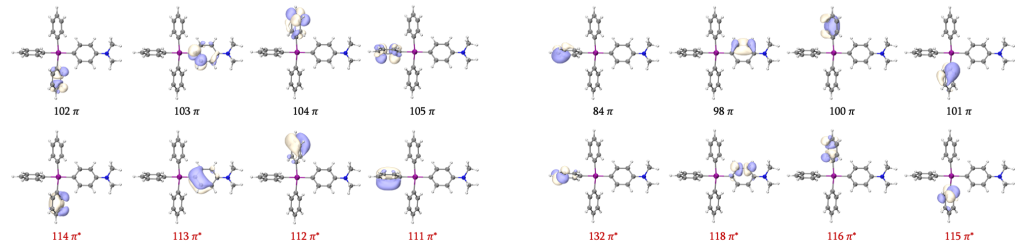
根据以上讨论,我们可以为RC (S = 3/2)构建三种不同大小的活性空间:
| Size of active space | Fe valence | Fe-phenyl σ/σ* | phenyl π/π* (1) | phenyl π/π* (2) |
| (11o,11e) | 107-109 | 46, 47, 58, 106 110, 158, 169, 170 | — | — |
| (19o,19e) | 107-109 | 46, 47, 58, 106 110, 158, 169, 170 | 102-105 111-114 | — |
| (27o,27e) | 107-109 | 46, 47, 58, 106 110, 158, 169, 170 | 102-105 111-114 | 84, 98, 100, 101 115, 116, 118, 132 |
3.2 TS-cross (S = 3/2)
在过渡态处,该交叉偶联反应的轨道表示如下:
2 (σ dsp2-LP) + 2 (σ* dsp2-LP) ⟶ (LP-LP σ) + (LP-LP σ*) + (LP-dsp2-LP 3c-2e) + (LP-dsp2-LP 3c-2e*)
我们可以找到对应于即将形成的C-C键的σ/σ*轨道,以及一组形如C-Fe-C三中心两电子键的轨道,以代替原有的两组Fe-C键的σ/σ*轨道。

除此之外,其他轨道均与RC (S = 3/2)类似,相应的三种不同尺寸的活性空间为:
| Size of active space | Fe valence | Fe-phenyl σ/σ* | phenyl π/π* (1) | phenyl π/π* (2) |
| (11o,11e) | 107-109 | 62, 63, 153, 154 106, 110 (C-Fe-C 3c-2e/3c-2e*) 43, 173 (C-C σ/σ*) | — | — |
| (19o,19e) | 107-109 | 62, 63, 153, 154 106, 110 (C-Fe-C 3c-2e/3c-2e*) 43, 173 (C-C σ/σ*) | 102-105 111-114 | — |
| (27o,27e) | 107-109 | 62, 63, 153, 154 106, 110 (C-Fe-C 3c-2e/3c-2e*) 43, 173 (C-C σ/σ*) | 102-105 111-114 | 77, 81, 99, 101 115, 117, 135, 139 |
3.3 MC-PDFT
选择以上活性空间后,我们已经可以对RC和TS进行(DMRG-)CASSCF计算,并基于CASSCF波函数进行MC-PDFT计算,从而得到反应的能垒。(DMRG-)CASSCF计算的流程可以仿照前文完成,计算结束后,得到自然轨道*NO.fch,观察收敛后的轨道是否合理。然后读取自然轨道做MC-PDFT计算:
bas_fch2py *NO.fch在得到的*NO.py结尾添加MC-PDFT计算的相关代码(可通过automr做一个小任务得到模板):
mc = mcpdft.CASCI(mf,'tPBE',19,(11,8)) # 可选的泛函形式参考PySCF说明文档。
mc.grids.atom_grid = (99,590)
mc.max_memory = 48000 # MB
mc.fcisolver = dmrgscf.DMRGCI(mol, maxM=1000)
mc.fcisolver.threads = nproc
mc.fcisolver.memory = 48 # GB
mc.kernel()对于本例,使用(11o,11e)活性空间得到的电子能垒仅约3 kcal·mol-1,这是明显不合理的,说明考虑苯环配体的π/π*轨道是必要的。使用(19o,19e)和(27o,27e)活性空间得到的电子能垒均在16 kcal·mol-1左右,这与原文的结果接近,也与实验结果比较符合。
3.4 P-cross/near (S = 1/2)
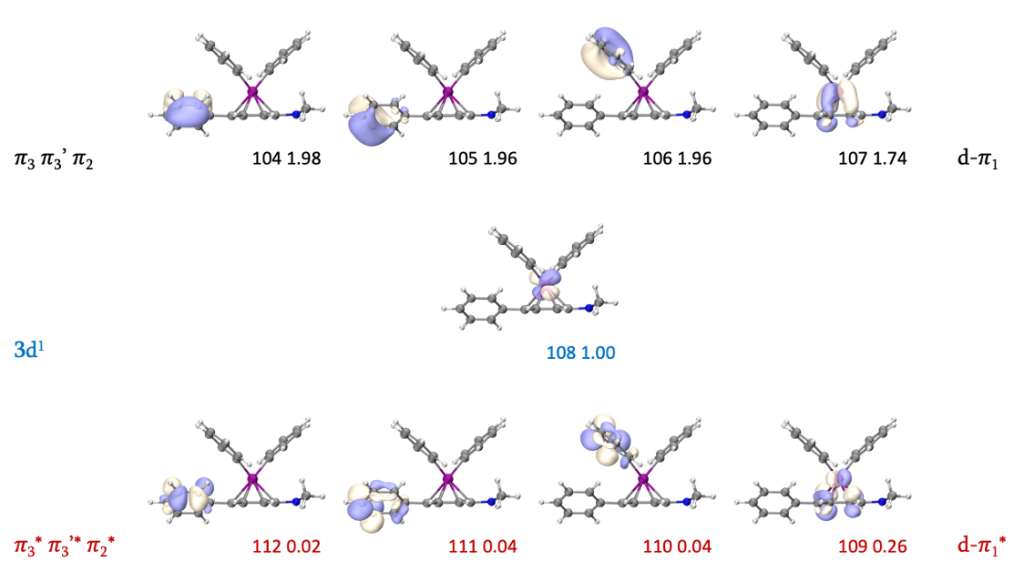
P-cross/near (S = 1/2)的结构中,偶联产物的一个苯环以π配体的形式与Fe(I)配位,因此该苯环的π轨道选择将会与RC和TS不同。我们首先确定其他三个苯环/苯基阴离子的π轨道。在占据数介于0.02-1.98范围的GVB轨道中,可以找到104-106和110-112共3组6个π/π*轨道。考虑到104、105、111和112属于同一个苯环,因此将105/111这一对π/π*轨道纳入(19o,19e)活性空间,104/112则纳入(27o,27e)活性空间。除此之外106/110也将其纳入(19o,19e)活性空间考虑。扩大轨道搜索的范围,还可以找到90、102、103、113、114和126,总计12个π/π*轨道,这就包含了这三个苯环/苯基阴离子需要纳入活性空间的全部π/π*轨道。
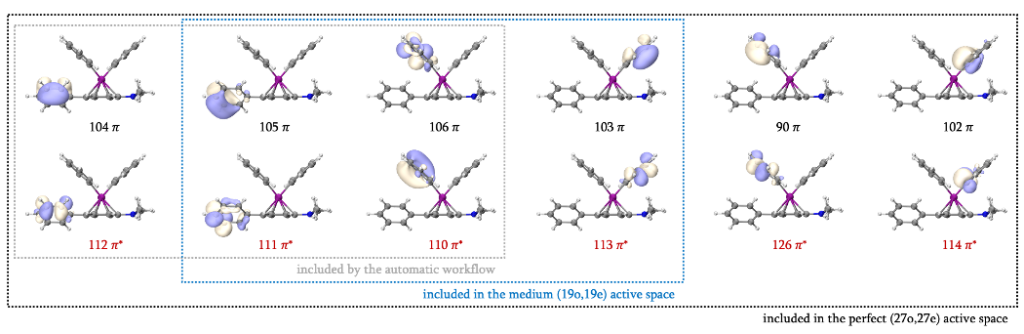
接下来我们确定另一个苯环的π/π*轨道。与二茂铁的GVB结果类似,部分轨道以Boys LMO的形式出现,此时我们首先需要排除σ/σ*轨道的干扰。苯环共有6组σ/σ*轨道,我们可以直接找到4组,分别是59、61-63、153-155和157,他们具有很明显的σ对称性。除此之外,还有48、64、67、74、78、138、142、149和152共9个轨道具有Boys LMO的形式,其中将会有2组σ/σ*轨道。观察已知的4组σ/σ*轨道,我们不难发现,有两根处于对位的C-C键未找到对应的σ/σ*轨道,故应在Boys LMO中找到分布在这两根C-C键上的轨道。参考二茂铁的处理方法,64/152和67/149是两组σ/σ*轨道,74/142和78/138则是两组π/π*轨道。
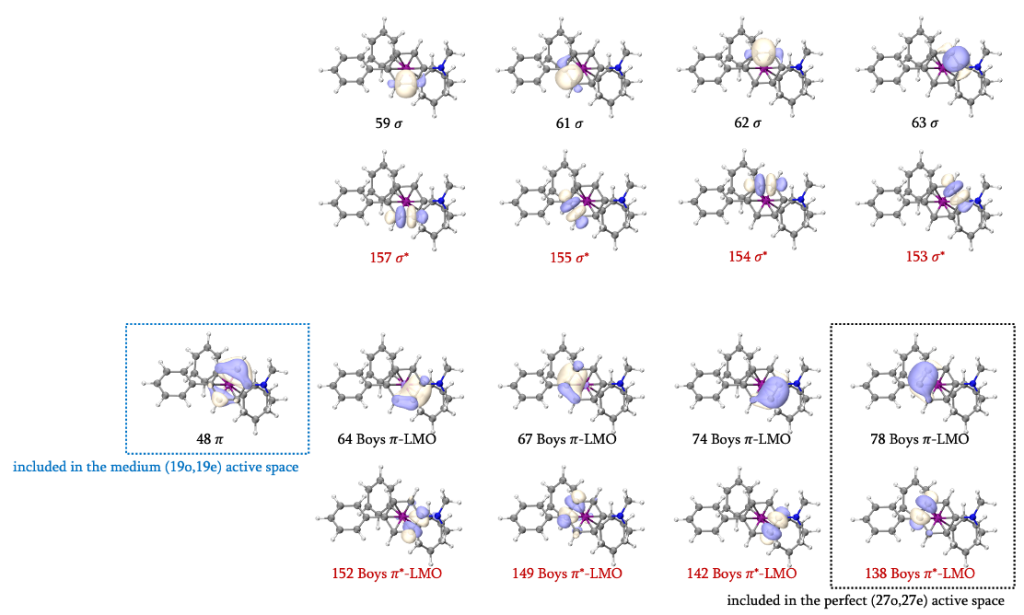
但我们会发现,48号轨道也是一个π轨道,但却并没有找到与其对应的π*轨道。考虑到SOMO为108号轨道,48号轨道的反键轨道理论上为108*2-48=168号轨道。但事实上观察168号轨道的等值面后会发现二者并没有直接联系,不具有化学意义上的成反键对应特征,因此该苯环确实缺少一个π*轨道。但观察占据数介于0.02-1.98之间的GVB轨道不难发现,107和109号轨道为d-π成反键轨道,且我们可以发现它们相位的分布形似“面对面”成键,若以通过Fe原子且平行于苯环的方向为z方向,这组轨道实际上是由dxz(或dyz)与π*轨道相互作用形成。在RC (S = 3/2)中,dxz和dyz均为单占轨道,还原消除后,二者均近似为为双占轨道,与π*轨道形成反馈键,呈低自旋态。因此我们就找到了缺失的π*轨道。
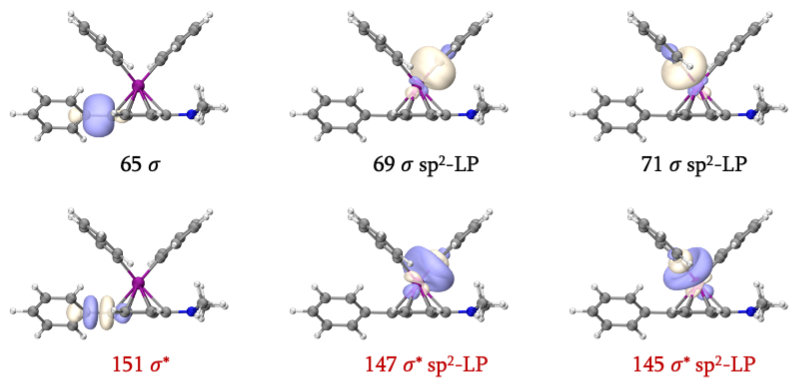
我们接着寻找反应物中的LP轨道。首先可以找到69、71、145和147,它们是反应过程中不变的Fe-C配位键轨道。由于新形成了一根C-C键,这包含两个原有的LP轨道及一对LP电子,因此考虑65和151号轨道后,原有的4个LP轨道就都被考虑进活性空间了。
接下来寻找Fe原子的价层轨道。由于产物中Fe原子的价态和配位形式都已经改变,此时实际上Fe原子采取dsp3杂化方式,这就使得我们在计算RC、TS和P时必须考虑全部4p轨道才能够比较能量。但杂化轨道本身并不存在,是化学家为了使成键方式更易于理解提出的一种模型,而GVB计算恰好体现了这一点,但在CASSCF计算中引入Fe原子的4s、4p轨道却并不必要。故此时GVB波函数作为CASSCF初猜的弱点就体现出来了。此外,GVB轨道在寻找Fe原子的价层轨道时,由于更高量子数基函数的混入,有时仅根据等值面形状会难于抉择,也依赖于很强的化学直觉和经验。我们亟需寻找一种简洁直白的工作流程来实现为一个反应选择统一的活性空间。
4. 为反应过程拟定统一的活性空间:片段组合方法
4.1 Fe催化交叉偶联
4.2 Fe/2-OGDC酶氧气活化
我们以Fe/2-OGDC酶氧气活化过程为例讲解我们的工作流程。对于该反应比较理想的活性空间应至少包括:Fe原子的全部3d轨道、O2的全部价层轨道、2-OG的C1-C2 σ/σ*轨道(涉及脱羧)、C1羧基两个氧原子的LP(脱羧后与原C1-C2 σ*共同形成CO2的一组π34)和C2-O π/π*轨道(涉及氧自由基进攻);总共是(5o,6e)+(8o,12e)+(6o,8e)=(19o,26e)。此外,纳入HIS的π/π*轨道也会对结果有所改进,但考虑到(23o,30e)的计算量过大,我们此处暂不将其纳入活性空间考虑。

