amb2gjf.py: 静电嵌入的QM/MM方法
amb2gjf.py: QM/MM Method with Electrostatic Embedding Scheme
Jiawei Xu, Yingqi Li
Released: 2024-05-13 / Updated: 2024-05-13
静电嵌入(electrostatic embedding, EE)的QM/MM方法是目前普遍使用的一种嵌入方法,即在计算QM区时MM区以背景电荷形式呈现,同时对QM/MM连接处的背景电荷和连接原子(linker atom)做特殊处理。本文简单回顾静电嵌入方法处理边界情况的基本原理,并介绍基于AMBER格式的参数,生成Gaussian输入文件,并按静电嵌入方法添加背景电荷设置的脚本amb2gjf.py。
1. 静电嵌入方法对边界的处理
1.1 连接原子
本文仅讨论使用氢原子作为连接原子的情况。
当QM/MM边界通过化学键相连时,切断边界导致QM和MM区的边界原子成键不饱和,需要添加连接原子保持结构的完整性。切断化学键、补全连接原子的目的是为了尽可能减少分层设置对QM和MM区产生的影响,尤其是不能对QM区的电子结构产生显著定量影响或定性影响。因此,常规的做法是切断共价成分高、极性低的化学键,并用氢原子作为连接原子(如图1所示)。在生物体系的研究中,一般是切断氨基酸的alpha-C和beta-C之间的碳碳单键,对于涉及核酸的情况,若有必要将磷酸基团保留在QM区域,也有可能切断3′,5′-磷酸二酯结构中的C-O单键,并补全为-OH。
连接原子的位置取决于被切断的化学键。考虑被切断的化学键的成键原子为QM区的A原子和MM区的B原子,其共价半径分别为r_{\text{A}}和r_{\text{B}},连接原子的共价半径为r_{\text{L}}(一般使用氢原子),则A-L键键长R为:
$$ R = g \cdot r \tag{1} $$
其中r为原A-B键长,比例系数g:
$$ g = \frac{r_{\text{A}} + r_{\text{L}}}{r_{\text{A}} + r_{\text{B}}} \tag{2} $$
1.2 背景电荷处理
我们将截断的化学键称作QM/MM键,如图1,QM区域的原子称为QM原子,与QM原子直接相连的MM区原子为MM1原子,与MM1原子直接相连的MM区原子为MM2原子,以此类推。由于QM/MM键被截断,QM原子使用连接原子L封端,故而MM原子的电荷通常需要进行特殊处理,以确保其对模拟结果的不利影响尽可能小。
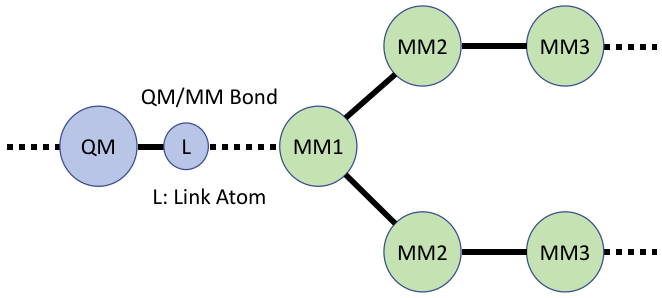
图1. QM/MM边界上的原子分类。
1.2.1 不处理背景电荷
保留全部MM区域的原子电荷作为背景电荷加入QM计算。此时,由于QM/MM键截断后使用L封端,L与MM1的距离往往过近,导致L受到不合理的静电作用。考虑到这一点,有必要对背景电荷进行处理,才能较为准确地在QM计算中重现边界附近的电子结构。
1.2.2 Zn方法
既然MM原子电荷与L过近会产生不合理静电作用,那么就直接忽略n层MM原子的电荷。如图2所示,Z1方法表示忽略所有MM1原子的电荷(用灰色表示),Z2方法忽略所有MM1、MM2原子的电荷,以此类推。该方法能够避免不合理的静电作用,但会导致整个体系的电荷不守恒,且局部静电势、偶极矩情况与实际不符。由于忽略更多层电荷并没有很明确的物理意义,Z2和Z3方法使用并不如Z1方法使用广泛。
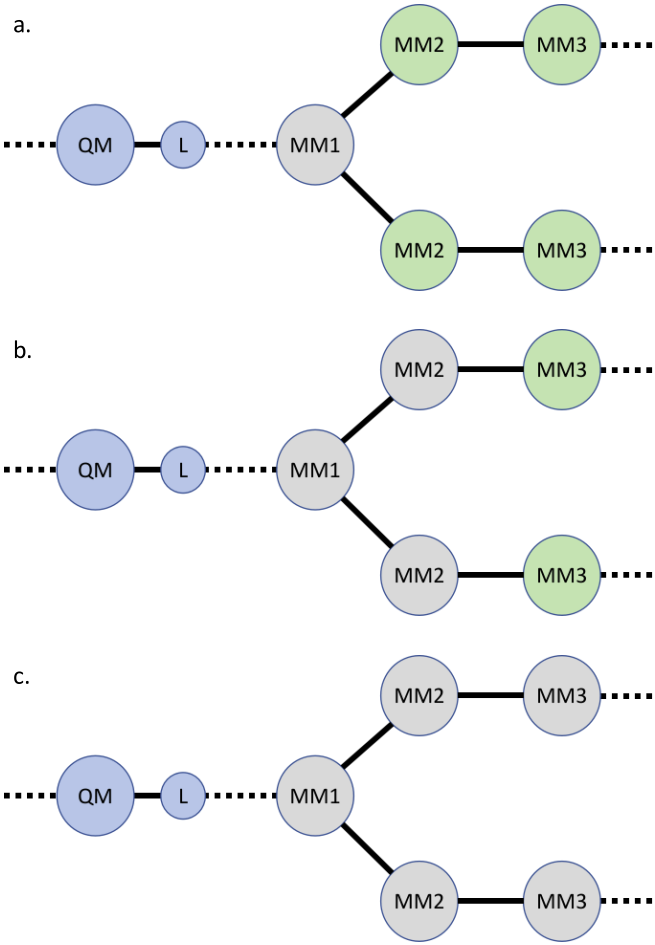
图2. a). Z1方法;b). Z2方法和c). Z3方法对边界附近电荷的处理。
1.2.3 重组电荷和偶极矩(redistributed charge and dipole, RCD)
为了避免Zn方法的缺陷,RCD方法将MM1原子的电荷沿MM1-MM2键轴向MM2原子方向移动,使之适当地远离L原子。考虑MM1原子电荷为q,与之直接相连的MM2原子个数为n的情况,假设移动后的电荷为q'。为了重现MM1-MM2键上的偶极矩,MM2原子的电荷也需要适当调整,假设其变化量为\Delta q,根据电荷守恒:
$$ nq’ + n\Delta q = q \tag{3} $$
调整电荷前后的偶极矩相等:
$$ \frac{q}{n} \cdot R_{\text{MM1-MM2}} = q’R_{q’-\text{MM2}} \tag{4} $$
其中R_{\text{MM1-MM2}}为MM1-MM2键长,R_{q'-\text{MM2}}为移动后点电荷与相应MM2原子之间的距离。上述两式的解不唯一,一般选MM1-MM2键轴中点作为移动后背景电荷的位置,即:
$$R_{q’-\text{MM2}} = \frac{1}{2} R_{\text{MM1-MM2}} \tag{5} $$
则可得:
$$q’ = 2\times \frac{q}{n} \tag{6} $$
$$\Delta q = – \frac{q}{n} \tag{7} $$
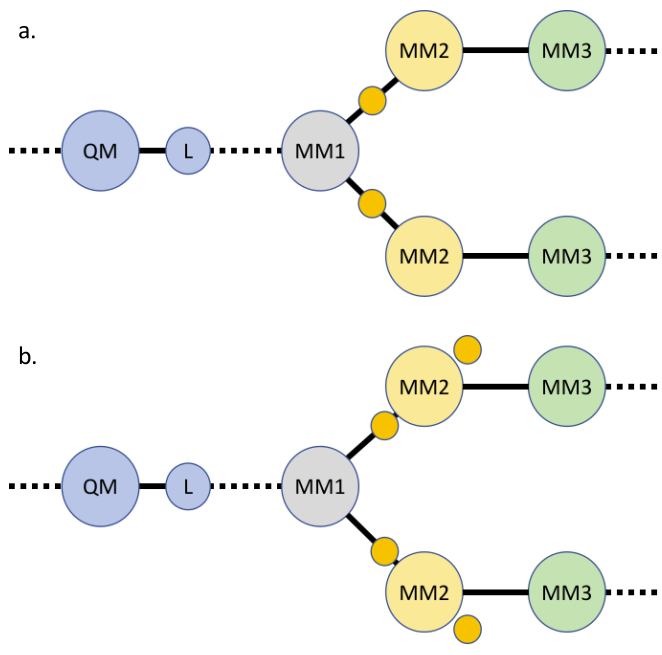
图3. a). RCD方法和b). CS方法对边界附近电荷的处理。黄色圆圈表示电荷发生了变化。
1.2.4 电荷移动(charge shifting, CS)
CS方法与RCD方法类似,但采用不同的分配策略。RCD方法采用“添加-扣除”策略,即先在MM1-MM2原子之间添加背景电荷,然后从MM2原子电荷中扣除相应的部分,以弥补新增的电荷,并重现局部的偶极矩。CS方法则采用“扣除-添加”策略,直接将MM1原子电荷加到与之相连的MM2原子上,由于MM1和MM2原子一般是带相反电荷的,因此实际上使得MM2原子的净电荷量减少,是一种扣除,该过程是电荷守恒的。为了重现偶极矩,沿着MM1-MM2键轴方向,在MM2原子前后各添加一对电荷量相等、符号相反的背景电荷+\delta q和-\delta q,其到MM2原子的距离为\delta r,则:
$$ \delta r \delta q = \frac{q}{n} \cdot R_{\text{MM1-MM2}} \tag{8} $$
显然,\delta q的具体数值也是依赖于距离\delta r的。不同的程序中对该距离有不同的产生方法,没有明显差异,一般来说会使\delta q更靠近MM2原子。
2. 使用方法
查看帮助:python amb2gjf.py -h;对于集群用户,实际上可以去掉后缀放在一个添加过环境变量的路径里,注明解释器,chmod +x amb2gjf,然后就可以作为命令调用了。
程序运行需要提供AMBER格式的参数文件,如test.prmtop和test.inpcrd,以及QM区的原子序号,默认使用CS方法处理边界上的电荷,并生成Gaussian格式的输出:
amb2gjf -i test -n "1-10 21-30 41-50" [-c cs -p g16]也可以通过-c选项指定其他的电荷处理方式,如:no(不做处理)、z1、z2、z3和rcd,具体含义参见前文。如此在当前目录下得到test.gjf,是一个包含了背景电荷设置的Gaussian输入文件,可以通过GaussView查看QM区的结构,检查选区是否正确,也可以用此进行带背景电荷的Gaussian单点计算。若需要ORCA格式的输入文件,则通过-p orca指定,将会得到.inp输入文件和带有背景电荷设置的pointcharges.xyz。

